A Brief Summary of Poisson Disk Sampling
I've been intending to write this post for almost two years now (since 2023-04). The topic and techniques described here have repeatedly surfaced in different contexts throughout the past years, and I've finally found time to sit down and summarize what I've learned on this subject so far.
When it comes to noise, it was fascinating to learn that people use colors to categorize different kinds of noise. Initially, I only knew about "white noise," as it was the most common pattern seen on TV when I was a kid if the signal was lost (the good old days).

It wasn't until I started my Ph.D. and began exploring different types of random points that I learned about the term "blue noise" for uniformly distributed random points. I wondered why these distributions were associated with colors. After some research, I was surprised to discover that there are many colors of noise, and their use in representing randomness relates to the spectral properties of different colors. In computer graphics (CG), as far as I know, only three colors are commonly mentioned or used: white, blue, and pink. Below is a chart that summarizes their key characteristics:
| White Noise | Blue Noise | Pink Noise | |
|---|---|---|---|
| One-word summary | Random Uniformity | Anti-Clumping | Natural Randomness |
| Frequency Spectrum (energy) | Equal at all frequencies (flat spectrum) | Concentrated in high frequencies | Decreases with frequency |
| Points spatial Pattern | completely uncorrelated | maximally dispersed | balanced correlation |
| Use Case | basic random sampling | "pleasing" evenly distributed sampling | organic pattern simulation (CGI textures) 1 |
| Example Image |  |  |  |
"Blue noise" is used specifically to generate visually pleasing, evenly distributed points.
Compared to white and blue noise, "pink noise" is less commonly used and appears primarily in certain specialized sub-fields, such as terrain modeling (heightfields) or CGI textures.
(There are quite some Free blue noise textures available on the Internet as it is already a very mature and heavily investigated topic.)
The next question is HOW.
It is generally easy to generate "white noise" using common random algorithms and map it to 2D or 3D. Even when these points don't perfectly achieve equal distribution at all frequencies ("random uniformity"), it's usually acceptable since the scenarios where this type of randomness is needed are often quite tolerant of imperfections. You can simply implement it like this:
#include <iostream> #include <vector> #include <random> #include <ctime> // Structure to represent a 3D point struct Point3D { float x, y, z; }; // Function to generate random points in 3D space std::vector<Point3D> generateRandomPoints3D(int numPoints, float bounds = 1.0f) { std::vector<Point3D> points; // Initialize random number generator std::random_device rd; std::mt19937 gen(rd()); std::uniform_real_distribution<float> dist(-bounds, bounds); // Generate the requested number of points for (int i = 0; i < numPoints; i++) { points.emplace_back(dist(gen), dist(gen), dist(gen)); } return points; }
When discussing the term Poisson, there are three related concepts that I'm familiar with: Poisson Distribution, Poisson Sampling, and Poisson Disk Sampling. All three honor the same French mathematician Siméon Denis Poisson (1781-1840), whose pioneering work on stochastic processes and probability laid the groundwork for these concepts. Although the methods themselves evolved after his time, their names pay homage to his foundational contributions to randomness and statistical theory.
It wasn't until writing this post that I realized I had actually learned about the Poisson distribution during my undergraduate studies, though not in English —-- in Chinese, it's called 泊松分布. This distribution is directly derived from Poisson's work in probability theory and models the number of events occurring in a fixed interval, assuming these events happen independently at a constant average rate. This distribution is the most direct attribution to Poisson's work.
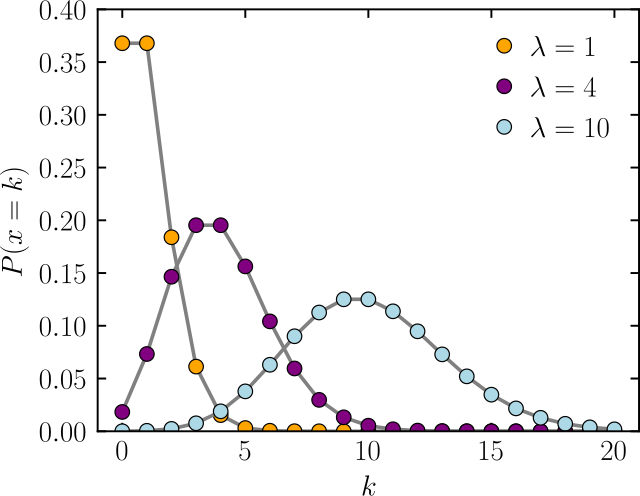
As this is not the main focus of this post, I will just put a Wikipedia link here reference.
The very first line on the Wikipedia page of Poisson Sampling is this:
Not to be confused with Poisson disk sampling.
It's rather amusing that I was actually one of those people who confused these two concepts initially. I first encountered this method during my master's studies at MIT and used the term incorrectly for many years until a postdoc during my PhD studies finally corrected me.
Before elaborating on Poisson Disk Sampling, let me first explain Poisson Sampling. This is a sampling method inspired by the Poisson Distribution. In survey statistics, for instance, "Poisson sampling" involves selecting units independently with individual probabilities, similar to the rare-event approximation of the Poisson distribution. While this technique was likely developed after Poisson's time, it is named in reference to his foundational work.
Here is a more comprehensive explanation from DeepSeek-R1:
Imagine you're picking people randomly from a crowd, but each person has their own independent chance of being chosen (like a lottery ticket). Unlike fixed-size sampling (e.g., picking exactly 100 people), Poisson Sampling lets the total number of selected items vary randomly. Each item is included or excluded based on its own probability, with no guarantee of how many you'll end up with. It's like flipping a (weighted) coin for every item to decide if it's in your sample.
The key take-away here is: Poisson Sampling is great when you want flexibility (no strict sample size) and independence (one person's selection doesn't affect another's). It's like rolling dice for every item in your population!
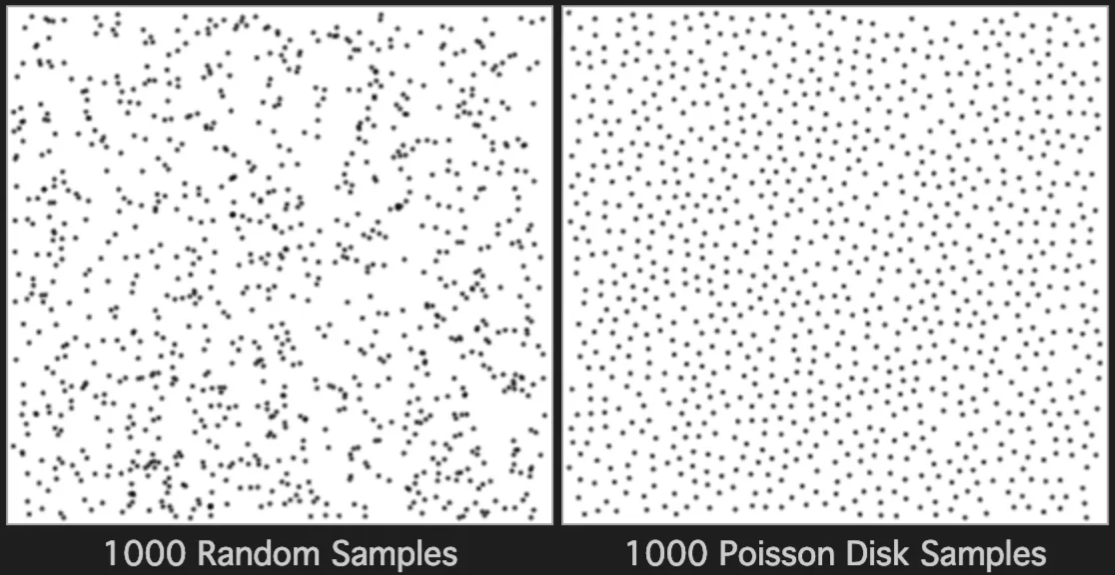
Now we finally arrive at the key concept I want to discuss in this post: Poisson Disk Sampling, which is one of the patterns of Supersampling. This is a spatial sampling method in CG where points are placed randomly, but no two points are closer than a specified distance (resembling a Poisson process with a minimum spacing constraint). The term "Poisson" here reflects the stochastic, non-gridded nature of the sampling (inspired by the Poisson process, itself named after Siméon Denis Poisson). The "disk" refers to the enforced minimum distance between points. Though this method was popularized in the 1980s, it builds on concepts tied to Poisson's foundational work.
I'd like to open a new section for this method below.
As mentioned above, this method was derived from Poisson sampling and has the characteristic of "no strict sample size."
To achieve the goal of "no two samples are too close," the most commonly used approach is to define a sample size , generate candidate points randomly using a so-called Dart-Throwing Algorithm, and only accept points that maintain a minimum distance from every previously accepted sample.
The criteria for selecting candidates is usually based on a "forbidden distance," within which no other candidate can exist. While initial researchers used a simple grid-based criteria and constrained the distance to , more sophisticated methods have been developed later. These include area-constrained approaches to more efficiently generate new candidates, or dynamic criteria to vary the "distance" (more on this in the Extended Topics section below).
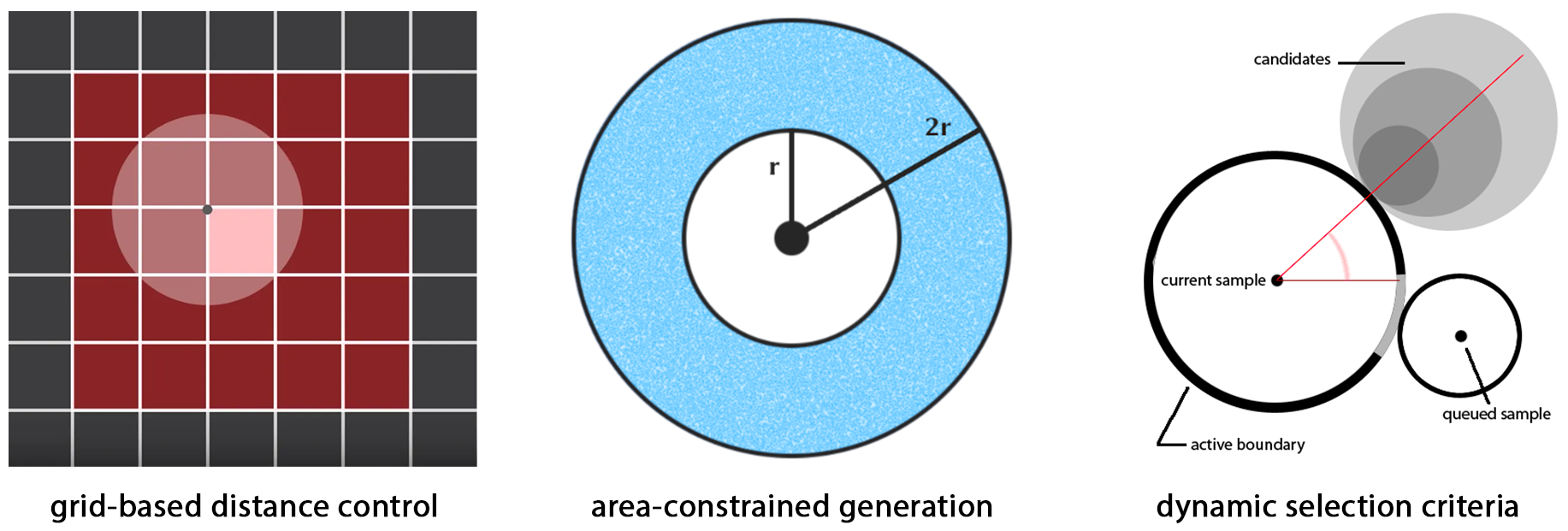
There are also efforts to improve the computational efficiency of the generation algorithm, the most famous of which is Fast Poisson Disk Sampling in Arbitrary Dimensions by Robert Bridson that runs in .
The main challenge with this approach is obtaining an exact number of samples within a given bound. Since the number of "selected candidates out of " is unpredictable, you either end up with a number that is close to but not exactly , or you need to iteratively run the algorithm with different values of until you reach your target . Alternatively, you can specify the constrained boundary and a target distance r between points, then let the algorithm fill the space and determine how many points you'll get.

Most available libraries and explanations follow this procedural approach. However, this doesn't satisfy the need to generate an evenly distributed random point set with a specific number of target points. Additionally, we often need to apply the method to higher dimensions and more complex shapes.
It's relatively straightforward to extend the method to dimensions, as the only criterion related to dimensionality is the cell size—by using as the cell size, you can directly obtain the point set in the target dimensions.
However, when it comes to manifolds, things become more challenging. While manifolds are a theoretical concept in mathematics, we can simply think of a 3D manifold as a smooth surface that can be locally approximated as a plane at any point.
Try to answer the question from the course CMU15-462/662 by Keenan Crane below:
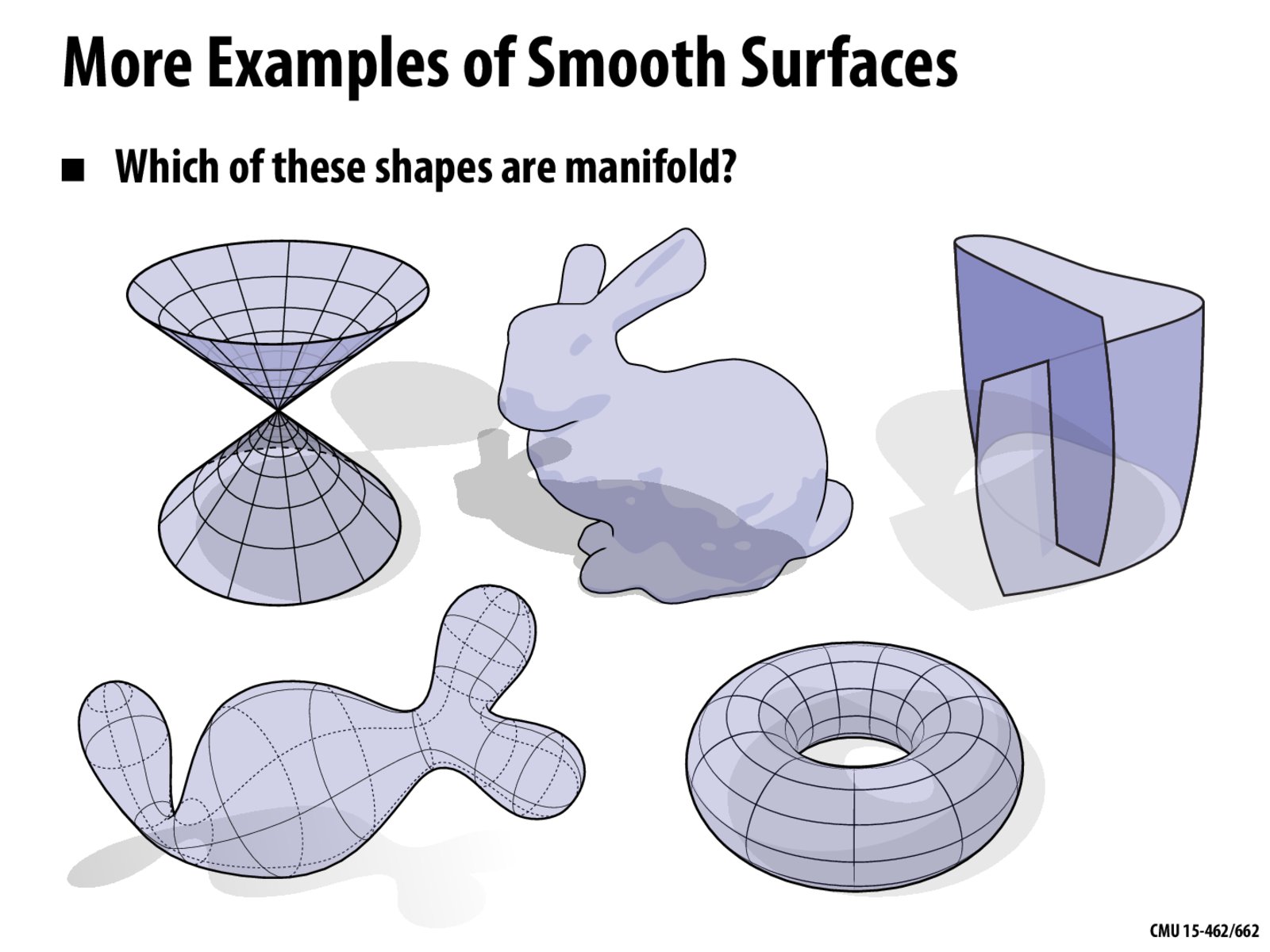
For simple primitive shapes like a sphere, we can use Mitchell's best-candidate algorithm to obtain a Poisson disk distribution, as demonstrated here. But for more general manifolds, I couldn't find any satisfactory papers or libraries until I discovered: Sample Elimination for Poisson Disk Sample Sets. The main author, Cem Yuksel, also provides a tutorial article for using his open-source library cyCodeBase that implements the method and explains the motivation behind developing it:
The problem with Poisson disk sample sets is that generating them has been notoriously difficult. This is because samples cannot be generated independently; each sample depends on the positions of the other samples. Simple algorithms (like dart throwing) are computationally expensive. Computationally efficient algorithms are complex and limited to certain sampling domains. High-dimensional sampling was practically impossible for anything beyond 6 or 7 dimensions.
This new approach introduces a "weight" to each candidate after randomly generating a reasonably large set of points (using a standard random process, which is fast), and then performs sample elimination based on those weights. This allows for a simple greedy algorithm for the elimination process, avoiding the less predictable iterative process when we need to obtain an exact number of points matching a given target.
One additional advantage of this approach is that you can use the target number of points as input, eliminating the need to specify a Poisson disk radius property (which is usually difficult to determine without running the algorithm several times to observe the results). For more interesting details and examples, I recommend reading the paper directly.
Since I couldn't find anything similar in the design community that uses Rhino/Grasshopper as its primary platform, I ported this method into the IG-Mesh plugin that I developed. Now designers can generate evenly distributed points on a 3D surface directly from Grasshopper:
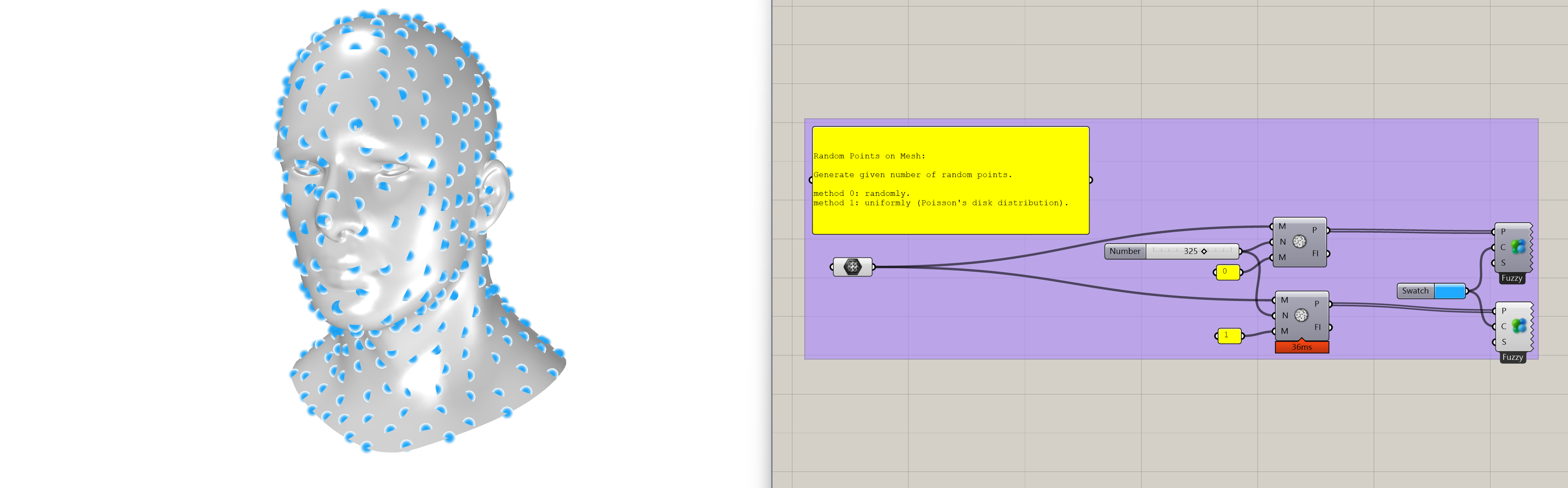
While Poisson Disk Sampling allows us to generate evenly distributed points on -dimensional manifolds, what are the use cases that make it so important? Beyond the various applications in rendering, plant generation, and other areas of CG, there are two related sub-fields that particularly connect to this method.
Before modern printing technologies were invented, books were typically printed using copper-plate engraving techniques. Artists would engrave text or drawings with crisp, precise lines on a copper plate, fill the etched lines with ink, and then print the design onto paper. A specialized technique called Stipple Engraving, within the broader intaglio printmaking tradition, uses fine needles, punches, or etching tools to create dots of various densities and sizes to control shading and texture. This approach can mimic the soft, tonal effects of chalk drawings or watercolors that traditional line-based engraving couldn't achieve.

As human society entered the Information Age, researchers in the computer graphics field began trying to replicate the effects of these traditional techniques for digital image styling. The algorithms used in such digital techniques are typically related to adaptive versions of Poisson Disk Sampling. For more information, I recommend reading A Survey of Digital Stippling.

There are also contemporary artists who still practice these traditional techniques to create stunning artworks:
Another interesting application for Poisson Disk Sampling is providing base point inputs for Voronoi Diagrams. This fascinating topic appears widely in nature, art, architecture, and many other fields—certainly worthy of a separate post. A Voronoi Diagram is the "dual" of a Delaunay Triangulation, and can be constructed efficiently given a set of points in -dimensional space.
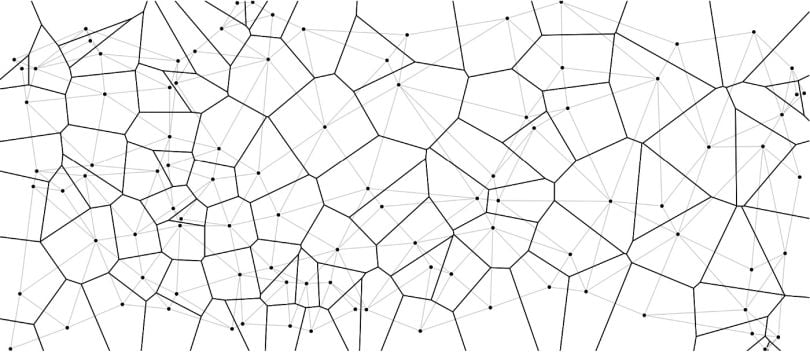
Since the diagram is entirely determined by its input points, we can think of it as following a "regular in, regular out; random in, random out" pattern, allowing us to control the resulting diagram by carefully selecting the input point set.

You can even build Voronoi diagrams on top of stippling points with varied density to create sophisticated applications in higher dimensions. Below is an example I developed for designing shoe soles with variable density based on pressure map data:
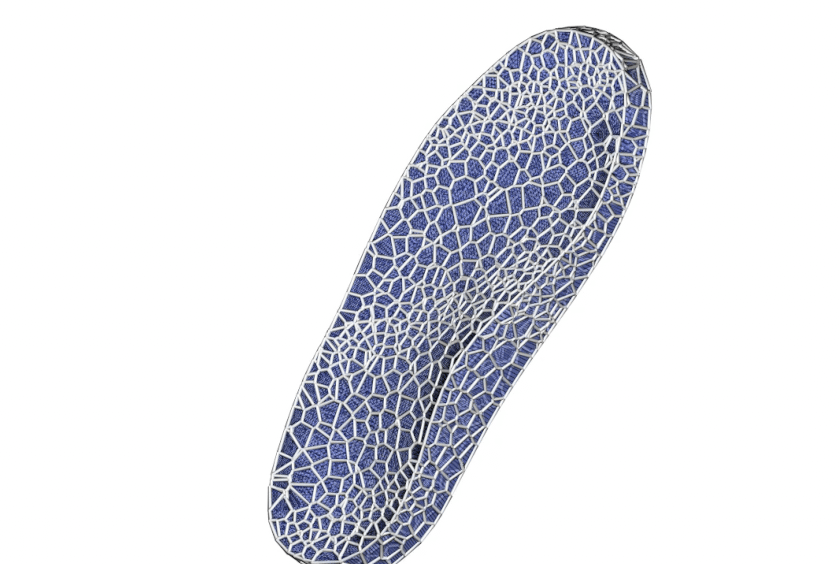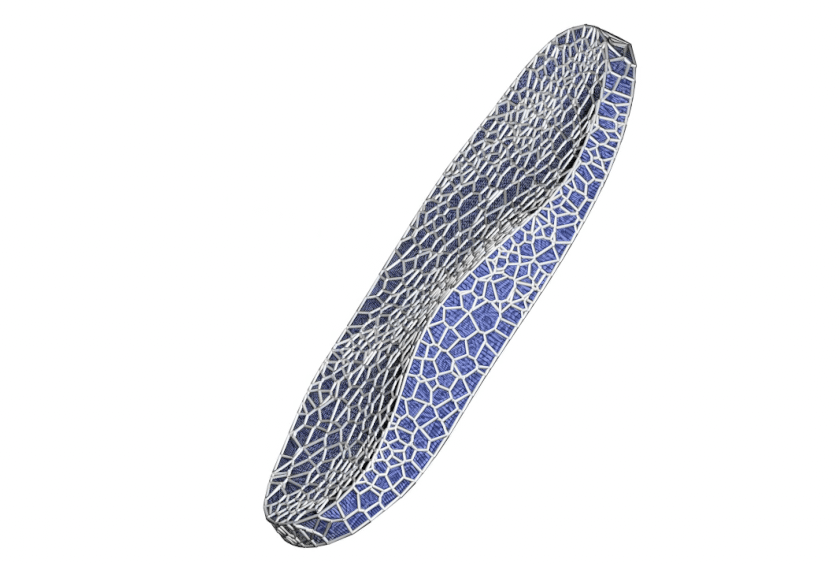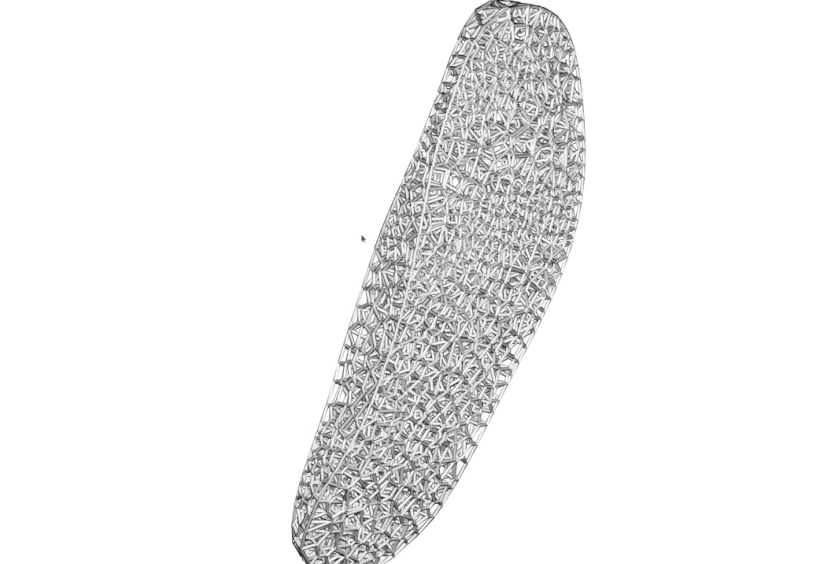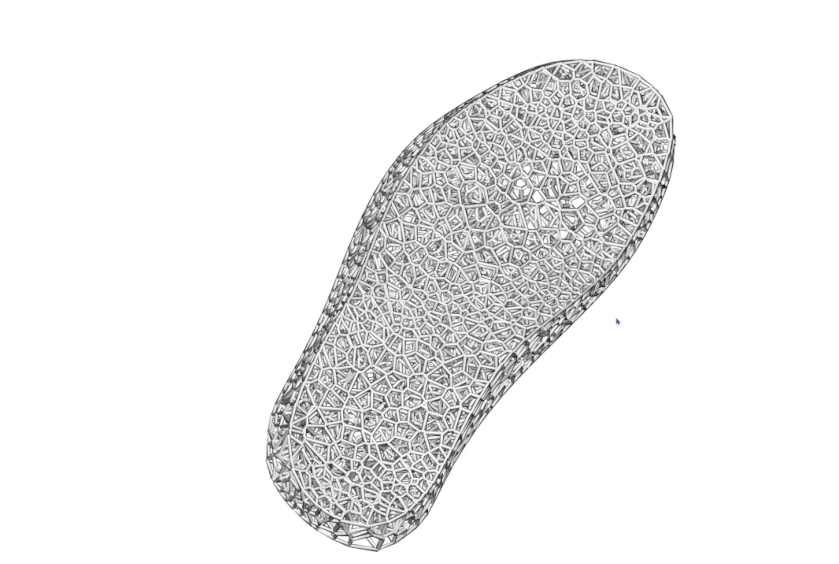
So there you have it -- my multi-year journey into the world of Poisson Disk Sampling finally wrapped up in one post. What started as a curiosity during my PhD has turned into one of those "once you see it, you can't unsee it" kind of things.
What I love most about this technique is how it sits right at that sweet spot between math and art. It's technically rigorous enough to satisfy my academic side, yet creates these visually stunning patterns that just feel right to the human eye. It's like nature's been using this algorithm all along, and we're just catching up.
I've had so much fun implementing this for my own projects (that shoe sole design was particularly satisfying), and I hope you'll find ways to play with it too. Whether you're rendering game scenes, designing architectural patterns, or just creating some cool digital art, this "Goldilocks" approach to randomness —- not too chaotic, not too rigid -— might be exactly what you're looking for.
- Javascript: Poisson-Disc Sampling by Jason Davies
- Javascript: poisson-disk-sampling (GitHub)
- Processing: Poisson Disk Sampling in Processing
- Python: PoissonDisk (Scipy Manual)
- C#: Variable Density Poisson-Disk Sampler
-
When it comes to texture or terrain generation in CG, another similar approach called [Perlin Noise] is more often used to generate realistic, smooth patterns by interpolating gradients on a grid. ↩